Talks

Talks displayed in this page are ordered by alphabetical order of the authors, with respect to their surnames. The schedule can be consulted on the schedule page.
The talks will take place at the lecture hall MA 141 in the mathematics building of the Technische Universität Berlin, at Straße des 17. Juni 136. More information about the location can be found on the venue page.
All talks have been recorded in video, but the video is released publicly only upon permission of the speaker; you can find the link to each video below the corresponding abstract. Some videos are only accessible with a password, which will be given out upon request. Unless noted otherwise below, you may contact the organisers directly.

Our conference will feature talks from two invited speakers and fifteen student speakers:

Plenary talks

Zeros of polynomials, from Descartes‘ Rule to P vs. NP

Olga Holtz (TU Berlin, UC Berkeley)

First algebraic methods for zero localization of polynomials go back to Descartes and Newton. But the story does not end there. Instead, it continues till today, leading to a number of recent advances such as the construction of Ramanujan graphs of every degree. I will review its humble beginnings and its rich connections to problems as varied — and as notorious — as the Riemann Hypothesis and P vs. NP.

More information about Olga Holtz can be found here.

Balanced manifolds or how to color a donut

Martina Juhnke-Kubitzke (University of Osnabrück)

The enumeration of faces of various types of simplicial complexes is a prominent topic in algebraic, topological and geometric combinatorics. In this talk, I will first provide a short survey on what is known for general simplicial complexes, simplicial polytopes and triangulations of manifolds. In the second part, the focus lies on balanced simplicial complexes, i.e., simplicial complexes whose underlying graph permits a minimal proper coloring in the graph-theoretic sense.

The video of the talk can be accessed in this link.

More information about Martina Juhnke-Kubitzke can be found here.

Student talks

Tropical Linear Algebra

Jorge Alberto Olarte (FU Berlin)

Tropical geometry is a relatively recent field that studies `polyhedral shadows' of algebraic varieties. In the tropical world there are many objects and theorems which are analogous to those in algebraic geometry. In this talk we will look specifically at tropical linear spaces and compare them with classical linear spaces. The main objective of the talk is to provide the audience with an understanding of what tropical linear spaces are, how do they look like and how do they relate to matroid polytopes. At the end I will briefly mention some results from the research that I have carried out with Alex Fink and with Marta Panizzut and Benjamin Schröter.

The video of the talk can be accessed in this link.

Counting projective planes

Simona Boyadzhiyska (FU Berlin)

A finite projective plane is a pair \((\mathcal{P},\mathcal{L})\), where \(\mathcal{P}\) is a finite set of elements, called points, and \(\mathcal{L}\) is a set of subsets of \(\mathcal{P}\), called lines, satisfying the following axioms:

  1. For any distinct \(p_1, p_2\in\mathcal{P}\), there is a unique \(\ell\in\mathcal{L}\) such that \(p_1,p_2\in\ell\).
  2. For any distinct \(\ell_1,\ell_2\in\mathcal{L}\), we have \(|\ell_1\cap\ell_2| = 1\).
  3. There exists a set of four points, no three of which belong to the same line.

It can be shown that if \((\mathcal{P},\mathcal{L})\) is a finite projective plane, then there exists a number \(n\in\mathbb{Z}_{\geq 2}\), called the order of the projective plane, such that any point is contained in exactly \(n+1\) lines, \(|\ell| = n+1\) for any \(\ell\in\mathcal{L}\), and \(|\mathcal{P}| = |\mathcal{L}| = n^2+n+1\).

Finite projective planes have been studied extensively, and yet some of the simplest and most natural questions related to them remain open or only partially answered. The first example of such a question is, given an integer \(n\), does there exist a projective plane of order \(n\)? Perhaps surprisingly, for many values of \(n\) the answer is still unknown.

Another interesting question we could ask is, what is the number of pairwise non-isomorphic projective planes of order \(n\)? In this talk, we will discuss some of the known results in this direction; in particular, we will see asymptotic lower and upper bounds on this number.

The video of the talk can be accessed in this link.

Hollow polytopes of large width

Giulia Codenotti (FU Berlin)

The aim of this talk is to present the construction of lattice polytopes of width larger than their dimension. After introducing lattice polytopes and some of their properties, such as width and hollowness, I will show how taking a direct sum of certain polytopes yields a hollow lattice polytope (resp. a hollow lattice simplex) of dimension \(14\) (resp. \(404\)) and of width \(15\) (resp. \(408\)). They are the first known hollow lattice polytopes of width larger than dimension. Asymptotic results can also be proved with this method, and will be touched upon if time allows. All terms introduced here (and more!) will be defined during the talk.

The video of the talk can be accessed in this link.

Grids of quadrilaterals with touching inscribed conics

Alexander Fairley (TU Berlin)

Conics are classical mathematical objects that have engendered many theorems. I will talk about a few theorems on the projective geometry of inscribed conics. In particular, I will present a theorem about grids of quadrilaterals with touching inscribed conics. Throughout the talk, there will be many illustrative computer graphics. At the end of the talk, I will mention current research about nets of planar quadrilaterals with touching inscribed conics.

The video of the talk can be accessed in this link.

Port-Hamiltonian systems

Candan Güdücü (TU Berlin)

The framework of port-Hamiltonian systems (PH systems) combines both the Hamiltonian approach and the network approach, by associating with the interconnection structure of the network model a geometric structure given by a Dirac structure. Furthermore, port-Hamiltonian systems theory is ideally suited for a systematic mathematical treatment of multi-physics systems by using energy and power as the lingua franca between different physical domains. A numerical method that exploits the structure of PH systems by using additive splitting methods has been derived. The results from a series of parametrized numerical experiments are presented to show the numerical stability and behavior of the solution depending on the parameters.

The video of the talk can be accessed in this link.

Exponential loss of memory for the stochastic Allen-Cahn equation with small noise

Tom Klose (TU Berlin)

We study the stochastic ordinary differential equation (SODE) $$\begin{align} \dot{u}_{\varepsilon}(t)& = -\nabla U(u_{\varepsilon}(t)) + \varepsilon\dot{w}(t), \tag{AC}\\ u_{\varepsilon}(0)& \in B(\pm 1,\delta), \end{align}$$ which is started in a small \(\delta\)-ball around \(+1\) or \(-1\), the stable equilibria of the double-well potential \(U(z) = \frac{1}{4}z^4 - \frac{1}{2} z^2\):

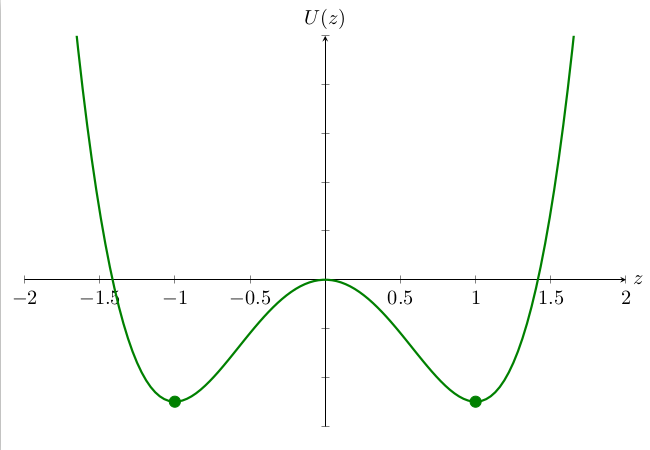
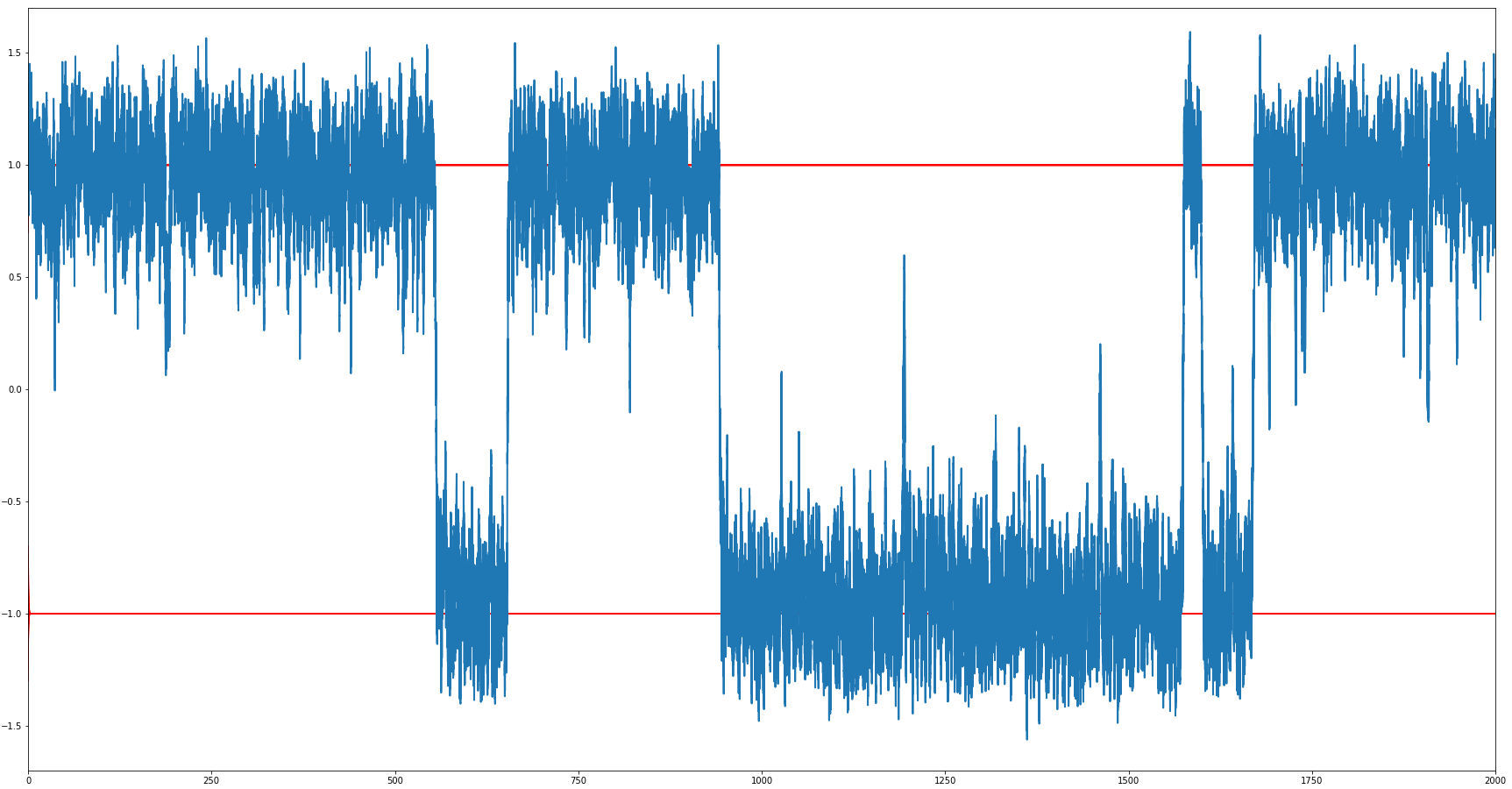
missing image
The double-well potential \(U\).

Under the presence of a temporal white noise \(\dot{w}\) with small intensity \(\varepsilon> 0\), solutions to (AC) exhibit metastable behaviour: they „jump“ between neighbourhoods of \(+1\) and \(-1\) (Figure b), a phenomenon completely different from deterministic dynamics (Figure a).

Change in behaviour of (AC) under the presence of temporal white noise \(\dot{w}_t\).
missing image
Figure (a): \(\varepsilon = 0\): the ODE case.
missing image
Figure (b): \(0 < \varepsilon \ll 1\): the SODE case.

Started from two different initial conditions \(u_{\varepsilon,1}(0), u_{\varepsilon, 2}(0) \in B(\pm 1, \delta)\), however, solutions to (AC) (in case \(\varepsilon >0\)) couple asymptotically with high probability: under the same random evolution, the equation „ loses memory“ of its initial condition exponentially fast.

I will make the preceding statement precise and outline the strategy of proof. Time permitting, I will discuss how the recent breakthrough in the study of singular stochastic partial differential equations (SPDE) allows to „tame infinities“ (Martin Hairer, Fields Medal 2014) using renormalisation techniques. We are then able to tackle the exponential loss of memory for the dynamic \(\Phi^4_3\) model formally given by the non-linear SPDE $$\begin{equation} (\partial_t - \Delta) \Phi_{\varepsilon}(t,x) = -\nabla U(\Phi_{\varepsilon}(t,x))+ \varepsilon\xi(t,x),\tag{\(\Phi^4_3\)} \end{equation}$$ \((t,x) \in \mathbb{R}_+ \times \mathbb{T}^3\), which describes phase separation phenomena in statistical physics and serves as a toy model for Euclidean quantum field theory.

The latter is joint work in progress with Pavlos Tsatsoulis (MPI Leipzig).

The video of the talk can be accessed with a password in this link. Please contact the speaker directly.

Hamiltonian systems, symplectomorphisms and generalised diffeomorphisms

Lars T. Kreutzer (Albert Einstein Institute, Max Planck Society)

The study of Hamiltonian systems is central to much of modern physics. We will explore what physicists mean when they talk about a „theory“, how Hamiltonian systems are analysed and how this is related to generalised notions of diffeomorphisms.

The video of the talk can be accessed in this link.

The Fiber Theorem and the Nerve Theorem

Evgeniya Lagoda (FU Berlin)

In this talk we will look at the poset Fiber Theorem and the Nerve Theorem for simplicial complexes, which establish isomorphisms of homotopy groups of simplicial complexes under certain conditions and are important tools in topological combinatorics. We will also consider some applications of these theorems. This talk will mostly follow the article Nerves, fibres and homotopy groups by Anders Björner.

The video of the talk can be accessed in this link.

Parameterizing families of curves

Carlos Maestro Pérez (HU Berlin)

In geometry, a parameterization of a given object is a way of expressing its coordinate functions in terms of a series of parameters. For example, the sphere \(S^2=\{x^2+y^2+z^2=1\}\) can be described by the rational equations $$x(t)=\tfrac{2a}{a^2+b^2+1}\,,\quad y(t)=\tfrac{2b}{a^2+b^2+1}\,,\quad z(t)=\tfrac{a^2+b^2-1}{a^2+b^2+1}\,,$$ which depend on the parameter \(t=a+ib\in\mathbb{C}\cup\{\infty\}=\mathbb{P}_{\mathbb{C}}^1\). Equivalently, this fact can be expressed as the existence of a dominant rational map $$\mathbb{P}_{\mathbb{C}}^1\to S^2\,,\quad t\mapsto(x(t),y(t),z(t))\,,$$ that is, a map defined almost everywhere whose image covers almost all of the target space. Building on this idea, rational parameterizations in algebraic geometry are defined as dominant rational maps \(\mathbb{P}_{\mathbb{C}}^n\dashrightarrow X\) from some projective space to the object \(X\) we want to study. The case where \(X\) is a family of algebraic varieties — say, genus \(g\) curves — is particularly interesting: indeed, finding a parameterization of such a family would mean that almost every curve of genus \(g\) could be completely determined by just \(n\) complex numbers. Trying to assume as little background in algebraic geometry as possible, we will explore some of these constructions in low genera, as well as the beautiful geometry that is hidden behind them.

The video of the talk can be accessed in this link.

Simulating Hurricanes on Bunnies, Point Vortex Dynamics on Closed Surfaces

Marcel Padilla (TU Berlin)

If we get lazy and track fluid motion just as a set of points representing the whirls of the fluid we end up with point vortex dynamics. The main question now becomes: „how do these point vortices move by the whirls they induce?“ In my talk I will explain this for planar, spherical and bunny shaped planets. This M.S. thesis will also be a gentle introduction into fluid dynamics.

The video of the talk can be accessed in this link.

A recap on the history of point-based graphics

Martin Skrodzki (FU Berlin)

Point sets arise naturally in many kinds of 3D laser-based acquisition processes, like 3D scanning. As early as 1985, they have been recognized as fundamental shape representations in computer graphics. They have diverse applications, e.g. in face recognition, traffic accident analysis, or archeology.

Point set surfaces have a more than 15 years long history in geometry processing and computer graphics as they naturally arise in 3D acquisition processes. A guiding principle of these algorithms is the direct processing of raw scanning data without prior meshing — a principle that has a long-established history in classical numerical computations. However, their usage mostly restricts to full dimensional domains embedded in \(\mathbb{R}^2\) or \(\mathbb{R}^3\) and a thorough investigation of a differential geometric representation of point set surfaces and their properties is not available.

In this talk, I will give a brief overview on the central structures and algorithms of point-based graphics.

The video of the talk can be accessed in this link.

Signal-to-interference ratio percolation for Cox point processes

András Tóbiás (TU Berlin)

One of the main questions in wireless communications is long-range connectivity in large networks. In the field of continuum percolation, long-range connectivity is identified with percolation, i.e., the existence of infinite connected components in random graphs in \(\mathbb R^d\), \(d \geq 2\). This field was introduced by Gilbert in 1961, who assumed that users of the network form a homogeneous Poisson point process, and that two users are connected if and only if their distance is less than a given constant \(r>0\). This model can be made more realistic in various ways. First, the locations of users should follow a street system, instead of a homogeneous spatial distribution. This setting was recently investigated by Hirsch, Jahnel and Cali, who studied Gilbert's graph model for Cox point processes, i.e., Poisson point processes with a random intensity measure. Second, connections should not only depend on the distance between transmitter and receiver, but also on the interference coming from all other users. Signal-to-interference plus noise ratio (SINR) percolation is a variant of continuum percolation having this property, which was studied by Dousse et al. in case of users given by a Poisson point process for \(d=2\). They showed that if the spatial density of users is high enough, then the SINR graph has an infinite connected component if interferences are sufficiently reduced (without vanishing).

In my talk, I will sketch these preliminary results, and afterwards I will tell about my research on SINR percolation for Cox point processes for \(d \geq 2\). I will show that under certain conditions on the intensity measure of the Cox point process and on the path-loss function, the SINR graph percolates if the user density is large and interferences are sufficiently cancelled. In particular, I will explain the case of the two-dimensional Poisson--Voronoi tessellation, which is one of the most realistic models for random street systems.

The video of the talk can be accessed in this link.

How many zeros does a random fewnomial system have?

Josué Tonelli-Cueto (TU Berlin)

A fewnomial system in \(n\) variables with \(t\) terms is a polynomial system \(f_1(x)=0,\ldots,f_n(x)=0\) of equations where each polynomial \(f_i\) in the system has a prescribed set of monomials described by a set \(A\subseteq \mathbb{N}^n\) of cardinality \(t\). In 1980, Khovanskii proved that such a system with real coefficients has at most $$ 2^{\binom{t-1}{2}}(n+1)^{t-1}$$ nondegenerate positive real solutions. It is important to note that this bound does not depend on the degrees of the polynomials. It is conjectured that this bound can be improved to be polynomial in \(t\). However, all existing improvements are still exponential in \(t\) .

In this talk, we consider a probabilistic version of this conjecture. We show that the expected number of nondegenerate positive real solutions of a random fewnomial system in \(n\) variables with \(t\) terms is bounded by $$ 2\binom{t}{n}, $$ which is polynomial in \(t\).

This is joint work with Peter Bürgisser and Alperen A. Ergür.

The video of the talk can be accessed in this link.

The Dimensionality of Point Clouds

Johannes von Lindheim (TU Berlin)

Manifold learning or nonlinear dimensionality reduction is concerned with the task of finding a \(d\)-dimensional parametrization of a \(D\)-dimensional data set (or point cloud) that is supported on a \(d\)-dimensional manifold, where typically \(d << D\). Almost all existing techniques, however, require the a priori unknown hyperparameter \(d\) called „intrinsic dimension“ (ID). Intrinsic dimension estimation is therefore concerned with finding this number of degrees of freedom in such a data set. We will see why that problem is difficult and consider a list of desiderata. I will present some relevant work in this field — however, to this day, there is no algorithm achieving all requirements of an „ideal“ intrinsic dimension estimator. Moreover, I will briefly touch upon an own ID estimator based on a novel approach using ideas from importance sampling.

The video of the talk can be accessed in this link.

An Experimental Classification of Maximal Mediated Sets and Their Relation to Nonnegativity

Oguzhan Yürük (TU Berlin)

In various real-world applications polynomial optimization plays an important role, and nonnegativity is an essential tool in polynomial optimization. Maximal mediated sets (MMS), first introduced by Bruce Reznick, arise as a natural structure in the study of nonnegative polynomials supported on circuits. Due to Reznick's, de Wolff's, and Iliman's results, given a nonnegative polynomial \(f\) supported on a circuit \(C\) with vertex set \(\Delta\), \(f\) is a sum of squares if and only if the non-vertex element of \(C\) is in the MMS of \(\Delta\). In this talk, we will first discuss the relation between MMS and nonnegative polynomials, and then present the results of the joint project with Olivia Röhrig and Timo de Wolff.

The video of the talk can be accessed in this link.